Основы учения о структуре кристаллов
Основы учения о структуре кристаллов
Основополагающим понятием в структуре кристаллов является представление о пространственной решетке. Пространственная решетка – это абстрактный геометрический образ, характеризующий наиболее общие закономерности расположения и периодичности повторения систем точек в пространстве.
Понятие это формировалось исторически. Пытаясь объяснить правильную геометрическую форму кристаллов, одни ученые (И. Кеплер, И. Ньютон, М.В. Ломоносов) исходили из того, что кристаллические многогранники образованы закономерной группировкой частиц шарообразной формы, другие (Р.Ж. Гаюи) – считали, что частицы, составляющие кристалл, имеют форму различных многогранников, складывающихся разным образом, наконец, третьи (В.Г. Волластон, М.П. Франкенгейм, А.А. Бравэ), абстрагируясь от морфологии частиц, рассматривали кристалл как систему из периодически чередующихся математических точек.
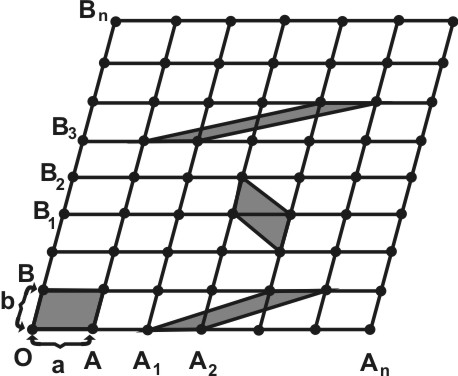
Для построения пространственной решетки достаточно задать в пространстве четыре точки (О, А, В, С) так, чтобы на одной прямой было не больше двух точек, а в одной плоскости – не больше трех. Другие точки, или как чаще говорят узлы решетки, выводятся из заданных путем параллельного переноса их по определенным направлениям (ОХ, OY, OZ).
В пространственной решетке все точки расположены по одинаковым параллельным рядам. Одномерным рядом пространственной решетки является любая прямая, проходящая через две произвольно выбранные (например, О и А) точки, на которой, кроме того, располагается бесконечное количество и других идентичных точек (А1, А2,…, Аn) на расстояниях, равных расстоянию между первыми двумя. Это кратчайшее расстояние между двумя одинаковыми точками называется периодом идентичности или промежутком (параметром) ряда. При перемещении точки А в точку А1 или точку О (т.е. вправо или влево) все одинаковые точки передвинуться на равные расстояния и ряд совместиться сам с собой, так что вид его не измениться. Эта операция называется трансляцией, представляющей новый вид симметрического преобразования, характерного для бесконечных пространственных решеток.
|
|
Одномерный ряд с трансляцией а. |
Если к одномерному ряду добавить произвольную трансляцию в направлении, не совпадающем с рядом, т.е. точки, лежащие на нем, повторить с помощью трансляции в произвольном направлении, то получим закономерное распределение точек на плоскости, которое называется двумерной решеткой или плоской сеткой. Плоская сетка определяется двумя элементарными трансляциями (а и b) или тремя узлами О, А, В не лежащими на одной прямой.
Эти три ближайших узла (О, А, В) располагаются в вершинах треугольника, являющегося половиной элементарного параллелограмма или ячейки сетки. Следовательно, плоскую сетку можно также определить как систему одинаковых элементарных параллелограммов, прилегающих и совмещающихся друг с другом с помощью параллельных переносов. Заметим, что элементарные параллелограммы – ячейки сетки можно выбрать по-разному (рис. 20). Параллелограммы, содержащие идентичные узлы только в вершинах, называются примитивными. Можно доказать, что площади различных примитивных параллелограммов для данной плоской сетки равны. В некоторых случаях элементарную ячейку выбирают так, что внутри ее оказывается дополнительный узел и она из примитивной делается сложной – центрированной.
|
|
Двумерная решетка с трансляциями a и b и разными элементарными параллелограммами. |
Все случаи симметрии плоских сеток исчерпываются пятью вариантами.
|
|
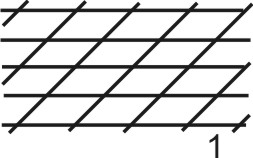
1. Плоская сетка образована с помощью двух неравных трансляций, пересекающихся в одной точке под углом, отличным от 90о. Симметрия случая a > < b; g > < 90о характеризуется наличием только L2 в центрах параллелограммов. |
|
|
2. Плоская сетка образована двумя трансляциями, пересекающимися под углом 90о. Если a > < b; g = 90о, то через оси L2 будут проходить две взаимоперпендикулярные плоскости. |
|
|
3. Плоская сетка в виде ромба образована двумя равными трансляциями, пересекающимися под углом, отличным от 90о. В этом случае (a = b; g > < 90о), так же как и в предыдущем варианте, через оси L2 будут проходить две взаимоперпендикулярные плоскости. |
|
|
4. Плоская сетка в виде примитивного квадрата образована двумя равными трансляциями, пересекающимися под углом 90о. Сетка имеет L4 и 4 P, проходящие через ось. |
|
|
5. Плоская сетка в виде примитивного ромба, короткая диагональ которого равна стороне, образована двумя равными трансляциями, пересекающимися под углом 60о. В случае a = b; g = 60о имеем симметрию L66P для узлов и L33P для центров треугольников (в этом случае поворот на 120о совмещает двумерную решетку саму с собой). |
|
Виды плоских сеток. |
|
Отсюда следует, что симметрия двумерных решеток допускает существование осей симметрии второго, третьего, четвертого и шестого порядков.
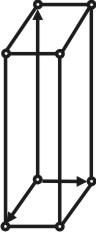
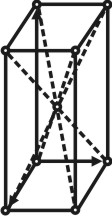
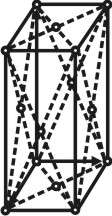
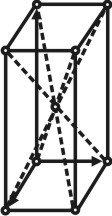
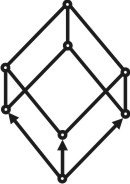
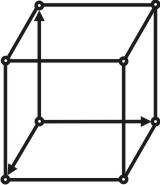
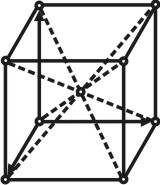
Любая плоская сетка в сочетании с трансляцией, взятой под углом, дает трехмерную пространственную решетку, определяемую тройкой элементарных некомпланарных трансляций. В зависимости от величин и взаимной ориентировки трансляций, пространственные решетки имеют различную симметрию. Каждую решетку можно разделить на множество параллелепипедов одинаковой величины, которые касаются друг друга целыми гранями и заполняют пространство без промежутков и которые могут быть совмещены друг с другом простым параллельным переносом (трансляцией). Такой параллелепипед называется элементарной ячейкой.
При выборе элементарной ячейки руководствуются некоторыми требованиями, позволяющими унифицировать подход к различным решеткам и максимально упростить их описание.
|
|
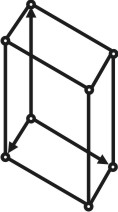
Пространственная решетка. |
Так, элементарная ячейка должна обладать: а) минимальным объемом; б) сингония ее – соответствовать сингонии всей решетки; в) число равных ребер и углов между ними должно быть максимальным; г) число прямых углов между ребрами – наибольшим.
Величины ребер элементарной ячейки обозначаются латинскими буквами a, b, c (соответственно координатными осями многогранников X, Y, Z); углы между ребрами – греческими буквами a, b, l, которые равны углам кристаллографических осей.
Ячейка называется примитивной или простой, если узлы решетки располагаются только в вершинах ячейки и сложной, если узлы решетки содержаться также где-либо внутри или на поверхности ячейки. Примитивная ячейка обозначается – Р. Среди сложных различают: объемоцентрированные – J (дополнительный узел в центре ячейки), гранецентрированные – F (дополнительные узлы в центре каждой грани), базоцентрированные – А, В, С (дополнительные узлы в серединах пары противоположных граней; А - центрированы грани первого пинакоида, В – второго и С – третьего пинакоидов) элементарные ячейки.
Примитивные элементарные ячейки, соответствующие кристаллографическим системам, можно получить из ранее рассмотренных плоских сеток путем прибавления к ним ортогональных и неортогональных трансляций. Неортогональная трансляция, добавленная к плоской сетке, образованной с помощью двух неравных трансляций, пересекающихся под углом, отличным от прямого (сетка 1), создает триклинную элементарную ячейку. В триклинном элементарном параллелепипеде величины основных трансляций различны a > < b > < c, углы a> <b > < l > <90о. Ортогональная трансляция, добавленная в такой плоской сетке, дает моноклинную элементарную ячейку, характеризующуюся следующими параметрами: a > < b > < c, углы a = l = 90о, b > < 90о. Если добавить перпендикулярную трансляцию к плоской сетке 2, образованной двумя неравными трансляциями, пересекающимися под углом 90о, то получим ромбическую элементарную ячейку, в которой a > < b > < c, углы a = b = l = 90о. Перпендикулярно направленная трансляция к сеткам, построенным из квадратов (сетка 4), образует два типа элементарных ячеек: тетрагональную, в которой a = b > < c, углы a = b = l = 90о или кубическую, в которой a = b = c; a = b = l = 90о в зависимости от того, равна ли или неравна добавленная трансляция с трансляцией, образующей квадрат. Ортогональная трансляция к плоской сетке в виде примитивного ромба (сетка 5) дает гексагональную или тригональную ячейку с параметрами a = b > < c, a = b = 90о, l = 120о. Прибавив к плоским сеткам 3 и 5 такую косую трансляцию, чтобы все три угла между ними были одинаковы, получим элементарную ячейку в виде ромбоэдра (a = b = c, a = b = l > < 90о). Такая тригональная решетка называется ромбоэдрической.
Из примитивных решеток, отвечающих различным кристаллографическим системам, М.Л. Франкенгейм (1835), а затем О. Бравэ (1850) вывели путем центрирования все 14 видов пространственных решеток.
14 видов решеток Бравэ.
|
|
Примитивная - P |
Базоцентрированная - С |
Объемоцентрированная -J |
Гранецентрированная – F |
|
Триклинная |
|
|
|
|
|
Моноклинная |
|
|
|
|
|
Ромбическая |
|
|
|
|
|
Тетрагональная |
|
|
|
|
|
Тригональная (ромбоэдрическая) |
|
|
|
|
|
Гексагональная |
|
|
|
|
|
Кубическая |
|
|
|
|