Элементы симметрии пространственных решеток
Элементы симметрии пространственных решеток
Симметрия пространственных решеток несравненно богаче симметрии кристаллов. К уже известным симметричным преобразованиям конечных фигур (кристаллов) при изучении симметрии пространственных решеток добавляются новые, основными из которых являются трансляции и такие сложные элементы симметрии, как плоскости скользящего отражения и винтовые оси симметрии.
Трансляция. Понятие "трансляция" означает перенос в данном направлении – перемещение в пространстве. Элементом симметрии, отвечающем такому симметрическому преобразованию будет ось трансляции. Для точной характеристики периодичности решетки необходимо указать направление трансляций и их величину. Заметим, что в литературе термин "трансляция" используется как для обозначения симметрического преобразования, так и элемента симметрии.
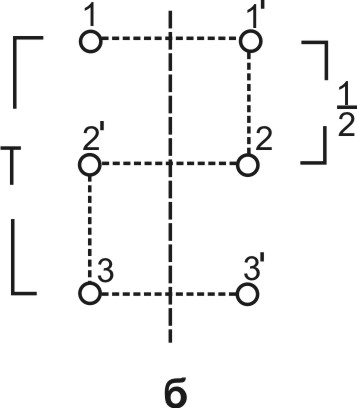
Плоскость скользящего отражения является комбинированным элементом симметрии, дающим симметричное повторение точки совместным действием зеркальной плоскости симметрии и трансляции.
Узел 1 (рис. б) отражается плоскостью симметрии и дает вспомогательное изображение 1', перемещенное одновременно на расстояние, равное половине периода идентичности в направлении трансляции, в результате чего имеем реальное симметричное изображение точки 1 в положении 2. В зависимости от того, с каким кристаллографическим направлением связана трансляция, плоскости скользящего отражения обозначаются различными символами: а, b, c, n и d. Плоскости скользящего отражения а, b и с обладают поступаниями, действующими параллельно первой (а), второй (b) и третьей (c) кристаллографическим осям соответственно. Величины поступаний ½a, ½b и ½с. Компоненты скольжения плоскостей n и d направлены по диагонали сторон элементарной ячейки и для поступаний n равны ½(b+c), ½(c+a), ½(a+b), а для поступаний d, соответственно ¼(b+c), ¼(c+a) и т.д.
|
|
|
|
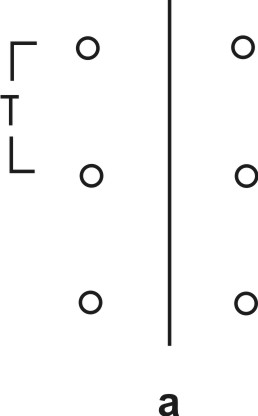
Действие обычной зеркальной (а) и плоскости скользящего отражения (б). |
|
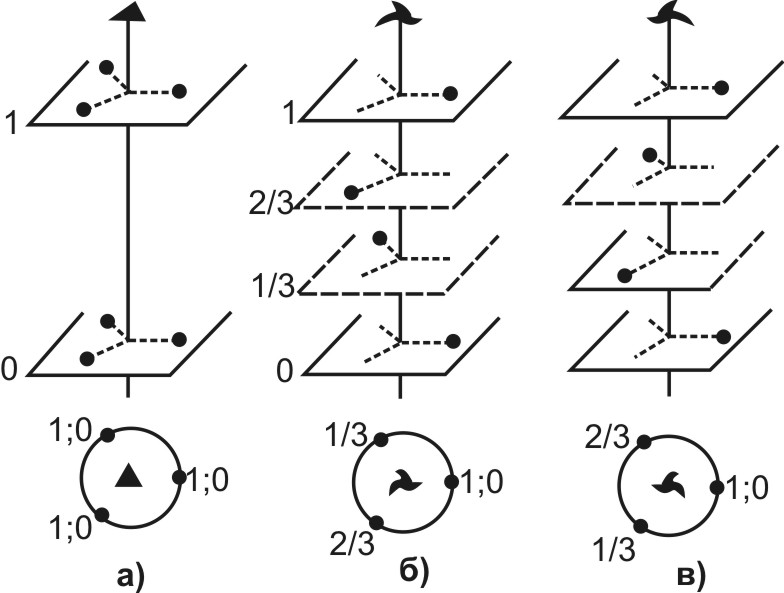
Винтовое вращение слагается из вращения и трансляции вдоль оси вращения. Элементом симметрии, соответствующим этой операции, является винтовая ось. При наличии винтовой оси n-го порядка, совмещение решетки самой с собой достигается поворотом ее вокруг этой оси на угол, кратный 360/n с последующим смещением вдоль оси на отрезок, кратный T/n, где T - период идентичности. На рис. показана тройная винтовая ось, которая дает симметричное повторение точки при повороте на 120о и перемещении на одну треть элементарной трансляции вдоль оси. Точка последовательно перемещается с уровня 1 до 2/3, 1/3 и 0. Нулевой уровень находится точно над точкой 1 на расстоянии T.
|
|
|
Оси симметрии третьего порядка: а) поворотная, б) винтовая правая 3,1, в) винтовая левая 3,2. |
Пространственные решетки могут обладать винтовыми осями второго, третьего, четвертого и шестого порядка и при этом различаться по величине трансляции. Существуют, кроме того, правые (поворот по часовой стрелке) и левые (поворот против часовой стрелки) винтовые оси. Двойная винтовая ось является одновременно и правой и левой. При описании структур кристаллов винтовые оси обозначаются следующим образом: 21, 31, 32, 41, 42, 43, 61, 62, 63, 64, 65. В этих обозначениях частное от деления маленькой цифры на большую, впереди стоящую, дает величину поступания вдоль оси по отношению к элементарной трансляции.
Поскольку пространственная решетка подразумевается бесконечной, то все элементы симметрии решеток, т.е. обычные плоскости симметрии и плоскости скользящего отражения, а также обычные поворотные и винтовые оси, будучи трансляционно повторенными, дают целые серии (семейства) аналогичных плоскостей и осей, параллельных самим себе. Все возможные сочетания элементов симметрии бесконечных пространственных решеток дают 230 комбинаций, называемых пространственными группами. Геометрический вывод всех пространственных групп был впервые выполнен в 1890 г. Е.С. Федоровым и вскоре, независимо от него А.М. Шенфлисом (1851) и В. Барлоу. Сравним: комбинируя элементы симметрии конечных фигур-кристаллов, получают 32 класса или вида симметрии кристаллов; комбинируя же элементы симметрии бесконечных фигур, выводят 230 пространственных групп симметрии.
Существует ряд способов обозначения пространственных групп. Наиболее рациональными являются обозначения Германа-Могена. Каждая пространственная группа содержит сначала обозначение, определяющее тип решетки Бравэ (P, J, F, A, B, C или R – ромбоэдрическая), затем следует обозначение класса, к которому относится данная пространственная группа; однако, иногда вместо буквы m, отвечающей зеркальной плоскости симметрии, могут применяться буквы a, b, c, n и d, показывающие наличие соответствующих плоскостей скользящего отражения, а вместо цифр 2, 3, 4 и 6, определяющих порядок поворотных осей симметрии, обозначения соответствующих винтовых осей. В качестве примера ниже приводятся символы видов симметрии по Бравэ, Герману-Могену и пространственных групп, являющихся разновидностями этих видов.
|
Виды симметрии |
Пространственная группа |
|
|
Бравэ |
Германа-Могена |
|
|
L2PC |
2/m |
P2/m; P2/n; C2/m; P2/c; P21/c; C2/c. |
|
L4PC |
4/m |
P4/m; P4/n; P42/m; P42/n; J4/m; J41/a. |
|
3L44L36L29PC |
m3m |
Pm3m; Pn3n; Pm3n; Pn3m; Fm3m; Fm3c; Fd3c; Jm3m; Ja3d. |
Отсюда видно, что от обозначения пространственных групп всегда легко можно перейти к обозначениям соответствующего ей вида симметрии. Для этого достаточно исключить большую букву (тип решетки Бравэ) и заменить символы винтовых осей на обычные поворотные, а плоскостей скользящего отражения на зеркальные.