Кристаллография и кристаллохимия

Геометрическая кристаллография.

Геометрическая кристаллография – изучает внешнюю форму кристаллов, законы симметрии кристаллов, сочетания различных форм и законы срастания кристаллов.

Понятия о симметрии

Симметрия (греч.)-соразмерность

Представление о симметрии широко развито в повседневной жизни.

Математическая разработка понятия о симметрии была разработана во второй половине 19 века.

В основе представления о симметричных фигурах лежит понятие о равных частях.

Симметрия (А.Ф. Мебиус): 2 фигуры называются взаимно равными, если для каждой точки одной фигуры имеется соответствующая точка другой фигуры, причем расстояния между двумя любыми точками одной фигуры равно расстоянию между 2-мя соответствующими точками другой фигуры.

Если одной точке А одной фигуры соответствует т.А₁ другой фигуры и расстояния между АВ и А₁В₁ одинаковые, то фигуры равны.

Ясно, что подобное определение справедливо и к любой части другой фигуры.

 Понятие равенства фигур, согласно данного определения значительно шире соответствующего понятия, принятого в элементарной геометрии..

В элементарной геометрии равными обычно называют такие фигуры, которые при наложении (или вложении) одна на другую совпадают всеми своими точками. Такие фигуры называют конгруэнтными (congruentis-совпадающий)

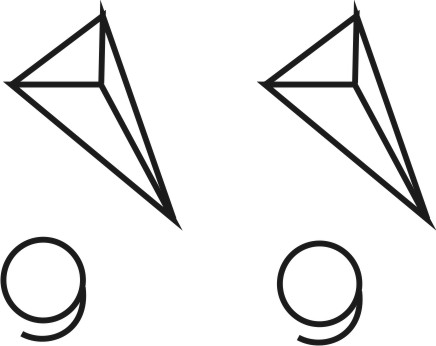
В кристаллографии равными считаются не только такие совместно равные фигуры, но так же и фигуры, относящиеся друг к другу как предмет и его зеркальное отображение.

Подобные фигуры, относящиеся друг к другу как предмет и его зеркальное отражение называются энантиоморфными

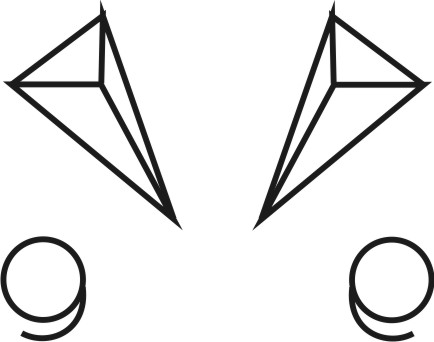
Симметричной называется такая фигура (многогранник) отдельные части которой могут быть совмещены друг с другом посредством симметричного преобразования.

Симметричным называется такое преобразование (отражение и вращение) в результате которого все равные части фигуры совмещаются друг с другом и фигура совмещается сама с собой.

Каждому симметричному преобразованию (т.е. действию) соответствует некоторый геометрический образ, называемый элементом симметрии. Иными словами: элементы симметрии - это вспомогательные геометрические образы, с помощью которых обнаруживается симметрии фигур.

Среди элементов симметрии различают элементы симметрии I и II рода.

Элементы симметрии I рода связывают друг с другом конгруэнтно равные фигуры (поворотные оси (симметрии) вращения).

Элементы симметрии II рода связывают друг с другом энантиоморфные фигуры. К ним относятся плоскости симметрии, центр инверсии и сложные оси симметрии (инверсионные)

Поворотная (простая) ось – это такая воображаемая прямая, проходящая через центр кристалла, при вращении вокруг которой определенные элементы многогранника повторяются n - количество раз, где n - порядок оси. То есть при повороте на некоторый угол совмещаются все одинаковые грани, ребра и вершины многогранника и он занимает в пространстве положение, эквивалентное исходному. В зависимости от минимального угла поворота (a), приводящего многогранник к самосовмещению, различают оси симметрии первого (a = 360^о, они обычно в расчет не принимаются), второго (a = 180^о), третьего (a = 120^о), четвертого (a = 90^о) и шестого (a = 60^о) порядков. В символике Бравэ ("учебной") оси симметрии обозначаются буквой L с цифровым индексом n, указывающем порядок оси – L₂, L₃, L₄, L₆ (соответственно – второго, третьего, четвертого и шестого порядков). В кристаллических многогранниках поворотные оси могут присутствовать в единственном числе или осей может быть несколько одного, либо разных порядков. Положение их в кристаллах видно на рисунке.

Многогранники с поворотными осями разных порядков.

 

Обычно выходы поворотных осей располагаются либо в центрах двух противоположных граней, серединах ребер и вершинах, либо проходят через вершину и центр грани. При этом надо учитывать, что в центрах граней прямоугольной или ромбовидной формы располагаются, как правило, выходы L₂, граней в виде равностороннего треугольника – L₃, квадрата – L₄ и шестиугольника – L₆. Через середины ребер проходят чаще всего оси второго порядка.

Плоскостью симметрии называется такая плоскость, которая делит фигуру на две зеркально-равные части, расположенные относительно друг друга как предмет и его зеркальное отражение. Обозначается она буквой Р (по Бравэ). Располагаются плоскости симметрии и ориентируются относительно друг друга в симметричной фигуре строго определенно, пересекаясь между собой, что наглядно видно на приводимом ниже рисунке.

Обычно они проходят через середины граней и ребер перпендикулярно им или же идут вдоль ребер, образуя равные углы с одинаковыми гранями и ребрами. В различных кристаллах плоскости симметрии присутствуют либо в единичном числе, либо в количестве двух, трех, четырех, пяти, шести, семи и девяти плоскостей.

Ориентировка плоскостей симметрии в различных многогранниках.

 

Центр инверсии (симметрии) – это воображаемая точка внутри кристалла, характеризующаяся тем, что любая, проведенная через нее прямая по обе стороны от нее и на равных расстояниях, встречает одинаковые элементы многогранника. Обозначается центр инверсии буквой С (по Бравэ). В многогранниках С всегда встречается в единственном числе – или он есть, или его нет.

Определить наличие центра инверсии у многогранников очень просто по следующему признаку: если каждой грани многогранника соответствует равная и параллельная (обратно-параллельная) грань, то он обладает центром инверсии, если хотя бы одной грани многогранника нет соответствующей равной и параллельной (обратно-параллельной) грани, то в нем С отсутствует. На рисунке приведены примеры кристаллов с центром инверсии (б) и без него (а).

Сложные оси симметрии.

Сложные оси симметрии позволяют совмещать равные части фигуры путем двойной операции: поворотом на некоторый определенный угол, задаваемый порядком оси, либо в плоскости перпендикулярной к оси вращения, либо точке на этой оси.

В первом случае ось называется зеркальной, во втором инверсионной

Инверсионной осью называется такая прямая линия, при повороте вокруг которой на некоторый определенный угол с последующим (или предварительным) отражением в центральной точке фигуры, как в центре инверсии, фигура совмещается сама с собой.

Подобный элемент симметрии представляет совокупность простой оси симметрии и центра инверсии, действующих не порознь, а совместно. При этом участвуя лишь в качестве составной части инверсионной оси, центр инверсии может не проявляться в виде самостоятельного элемента симметрии.

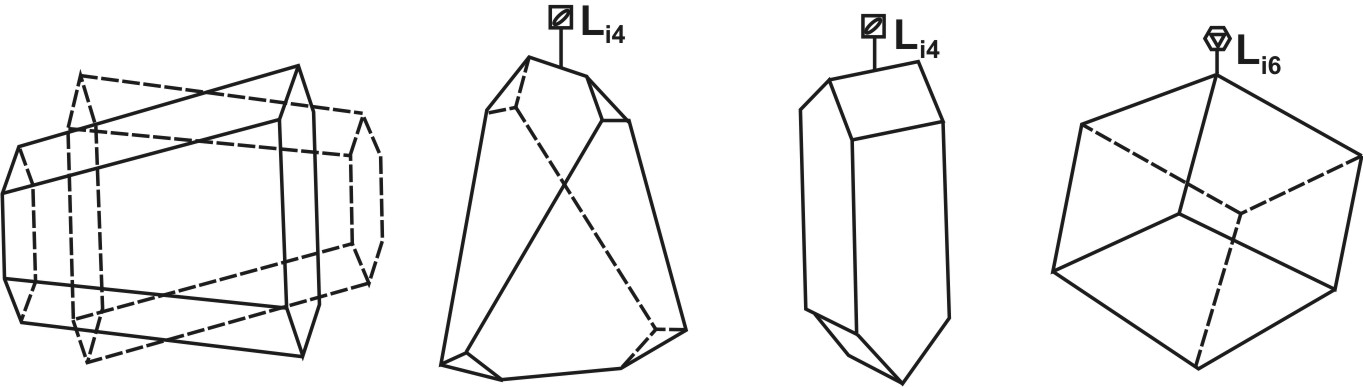
В качестве самостоятельных элементов симметрии важно определять лишь инверсионные оси симметрии четвертого и шестого порядков, обозначаемых L_i4 и L_i6 (по Бравэ). Другие инверсионные оси отвечают уже известным нам элементам симметрии, так L_i1 = C; L_i2 = Р (перпендикулярной к ней).

Из указанных осей (L_i4 и L_i6) с наибольшим трудом находится инверсионная ось четвертого порядка. Следует отметить, что L_i4 всегда совпадает с простой двойной осью симметрии. При этом в многогранниках с подобной инверсионной осью, совмещающихся сами с собой в результате совокупного действия простой оси симметрии и центра инверсии, действующих не порознь, а совместно, центр инверсии, выступая в качестве составной части этой оси, не проявляется в виде самостоятельного элемента симметрии. Вместе с тем не любая L₂ при отсутствии С отвечает L_i4. Шестерная инверсионная ось всегда равна поворотной тройной оси и плоскости нормальной к ней; центра инверсии в этом случае тоже нет. Если установлено наличие L₃ и Р, то указывать L_i6 не обязательно и наоборот. Таким образом, характеризуя симметрию кристаллов, достаточно установить следующие элементы: P, C, L₂, L₃, L₄, L₆, L_i4, L_i6 в обозначениях (по Бравэ).

Взаимодействие элементов симметрии

Указанные элементы симметрии встречаются в многогранниках совместно, причем сочетание их не является случайным, а вполне закономерным, т.к. элементы симметрии взаимосвязаны друг с другом.

Существует ряд теорем, позволяющих математически вывести все возможные совокупности элементов симметрии, и знание этих теорем может оказать значительную помощь при практическом определении элементов симметрии у многогранников.

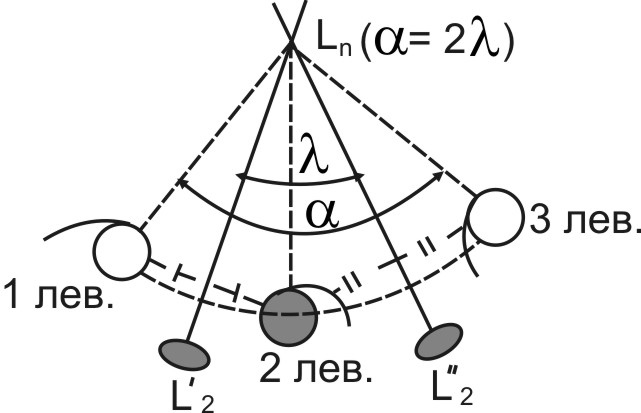
Теорема 1. При наличии двух пересекающихся осей симметрии присутствует третья равнодействующая ось симметрии, проходящая через точку их пересечения с элементарным углом поворота, вдвое превышающим угол между исходными осями.

Рис. 1. К теореме о двух пересекающихся осях.

 

Модельное доказательство. Ассиметричная фигурка 1 (рис. 1) переводится в положение 2 поворотом вокруг горизонтальной оси 2-го порядка (L'₂). Если фигурку условно назвать "левой" (в дальнейшем "левыми" будем называть фигурки, конгруэнтно равные первой, а "правыми" - энантиоморфно равные ей), то "левой" следует и назвать фигурку 2, которая после поворота покажет наблюдателю свою изнанку. Поворот фигурки 2 вокруг оси L''₂ переведет ее в положение 3, оставив по-прежнему "левой" (к наблюдателю снова обращена "лицевая" сторона фигурки). Две "левые" фигурки – 1 и 3 – равны конгруэнтно и расположены таким образом, что могут быть совмещены друг с другом поворотом вокруг вертикальной оси L_n на угол a = 2l (ось L_n ^ к плоскости чертежа).

Следствие. Если в кристалле перпендикулярно оси n-го порядка проходит ось 2-го порядка, то таких очей будет энное количество (т.е. такое количество, каков порядок оси – nL₂).

 

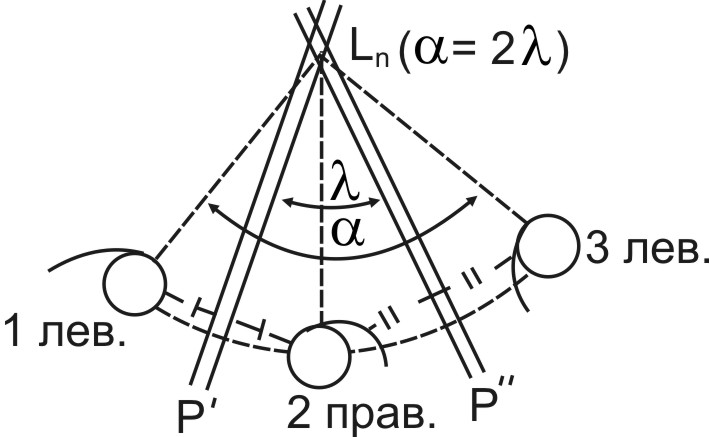
Теорема 2. Линия пересечения двух плоскостей симметрии есть простая ось симметрии, равнодействующая этих плоскостей. Элементарный угол поворота данной оси вдвое больше угла между плоскостями.

Рис. 2. К теореме о двух пересекающихся плоскостях.

 

Модельное доказательство. "Левая" фигурка 1 (рис. 2) переводится отражением в зеркальной плоскости p' в "правую" фигурку, которая, будучи отражена в плоскости p'', снова становиться "левой". Две "левые" фигурки 1 и 3 равны конгруэнтно и могут быть совмещены друг с другом поворотом на угол a = 2l вокруг оси Ln, нормальной к плоскости чертежа.

Следствие. Если через ось симметрии n-го порядка (Ln) проходит плоскость симметрии, то число плоскостей, проходящих через ось, равно порядку данной оси (nP).

 

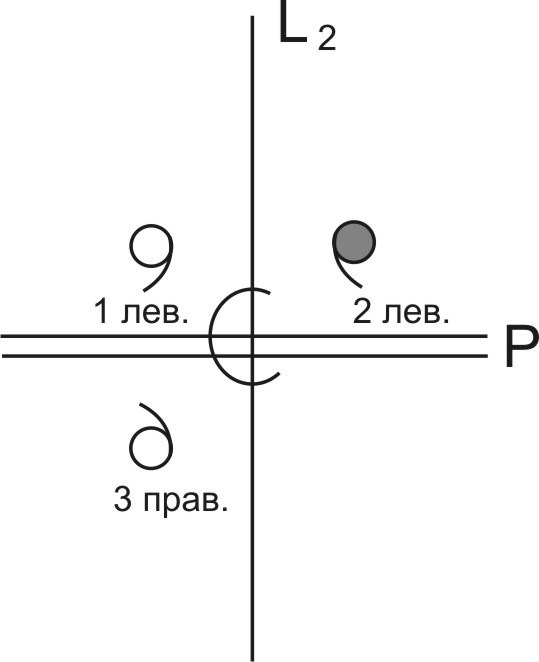
Теорема 3. При наличии простой оси симметрии четного порядка (L₂) и центра инверсии перпендикулярно к оси должна проходить плоскость симметрии.

Рис. 3. К теореме о наличии оси четного порядка и центра инверсии.

 

Модельное доказательство. "Левая" фигурка 1 в результате поворота вокруг оси L₂ переводиться в положение 2, поворачиваясь к наблюдателю изнанкой, но оставаясь "левой" (рис. 3). Отражение в центре инверсии переводит фигурку из положения 2 в положение 3, при этом она становиться "правой". Очевидно, что фигурка 1 из 1-го положения может быть непосредственно переведена в позицию 3 за счет отражения в плоскости нормальной к оси четного порядка. Поэтому действие плоскости равнозначно повороту на 180^о вокруг перпендикулярной к Р оси и последующего отражения в центре инверсии.

Следствие. При наличии центра инверсии сумма четных осей равна сумме плоскостей симметрии; причем каждая четная ось ^ плоскости симметрии.

 

В общем случае наличие 2-х из 3-х вышеуказанных элементов (С, Р, L₂) вызывает появление третьего. Так: а) при наличии С и проходящей через него Р, перпендикулярно последней находится четная ось; б) при наличии взаимно перпендикулярных L₂ и Р, всегда присутствует С.

Единичные и симметрично равные направления.

Единственное, не повторяющееся в кристалле направление называется единичным.

Повторяющиеся в кристалле направления, связанные элементами симметрии, называются симметрично-равными.

Количество единичных направлений в кристалле может быть различным.

В кубе любая прямая повторяется несколько раз. Следовательно, в этом многограннике единичные прямые отсутствуют, а существуют лишь симметрично-равные. Наоборот, в кристалле, не обладающем элементами симметрии, или содержащем только С, симметрично-равных прямых нет, здесь каждая прямая является единичной. В других кристаллах в зависимости от того, к каким видам симметрии они принадлежат, может быть разное количество симметрично-равных и единичных прямых.

Понятие о выводе простых форм

Формой многогранника называется совокупность всех его граней. Она определяется количеством всех сортов граней, взаимным расположением и соотношением размеров граней разного сорта. По внешнему виду кристаллы разделяются на две группы. К первой относятся такие кристаллы, которые состоят из одинаковых и симметрично расположенных граней (т.е. граней одного сорта). Они представляют собой простые формы. В простой форме все грани связаны между собой элементами симметрии и выводятся из одной заданной грани посредством этих элементов. Ко второй группе относятся кристаллы, обладающие различными по очертаниям и величине гранями (т.е. гранями разного сорта). Эти многогранники являются комбинациями, представляющими собой совокупность двух или нескольких простых форм. Количество простых форм, участвующих в сложении комбинационного многогранника, определяется количеством сортов граней. Всего известно 47 типов простых форм: 7 – для низшей категории, 25 – для средней и 15 – для высшей категории. Комбинаций возможно бесконечное количество.

Простые формы бывают открытыми и закрытыми. Закрытая форма может одна образовывать кристаллический многогранник, так как грани закрытой формы полностью замыкают заключенное между ними пространство. К ним относятся дипирамиды, тетраэдры, трапецоэдры и др. Одна открытая простая форма, которыми являются, например, диэдры, пинакоиды, пирамиды и призмы, замкнутого многогранника образовать не может. Кристалл в этих случаях сформирован гранями нескольких простых форм, дающих комбинацию (не исключено, что в комбинации могут входить и закрытые формы).

Кроме того, простые формы, в зависимости от положения граней относительно элементов симметрии, разделяются на частные и общие. Простая форма называется частной, если ее грань: 1) параллельна какому-нибудь элементу симметрии; 2) перпендикулярна какому-нибудь элементу симметрии; 3) образует одинаковые углы с двумя равными элементами симметрии. Простая форма является общей, если положение ее грани не удовлетворяет ни одному из приведенных выше трех условий.

Некоторые простые формы имеют две разновидности: правую и левую. Например, ромбические тетраэдры, все трапецоэдры, пентагон-тритетраэдры и др. Комбинационные многогранники также бывают правые и левые. Такие формы называют энантиоморфными (противоположно равными), это две зеркально равные фигуры, не совместимые друг с другом путем переносов и поворотов. Энантиоморфные формы возможны только в тех видах симметрии, в которых отсутствуют инверсионные оси, плоскости симметрии и центр инверсии.