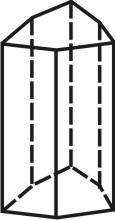
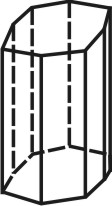
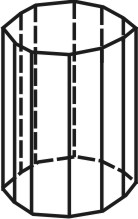
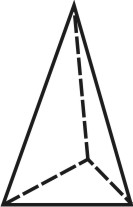
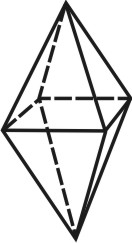
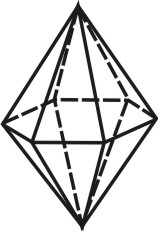
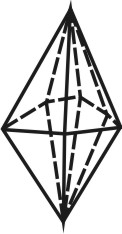
Кристаллография: Простые формы. | Образовательный портал "Электронный университет ВГУ"

Простые формы кристаллов

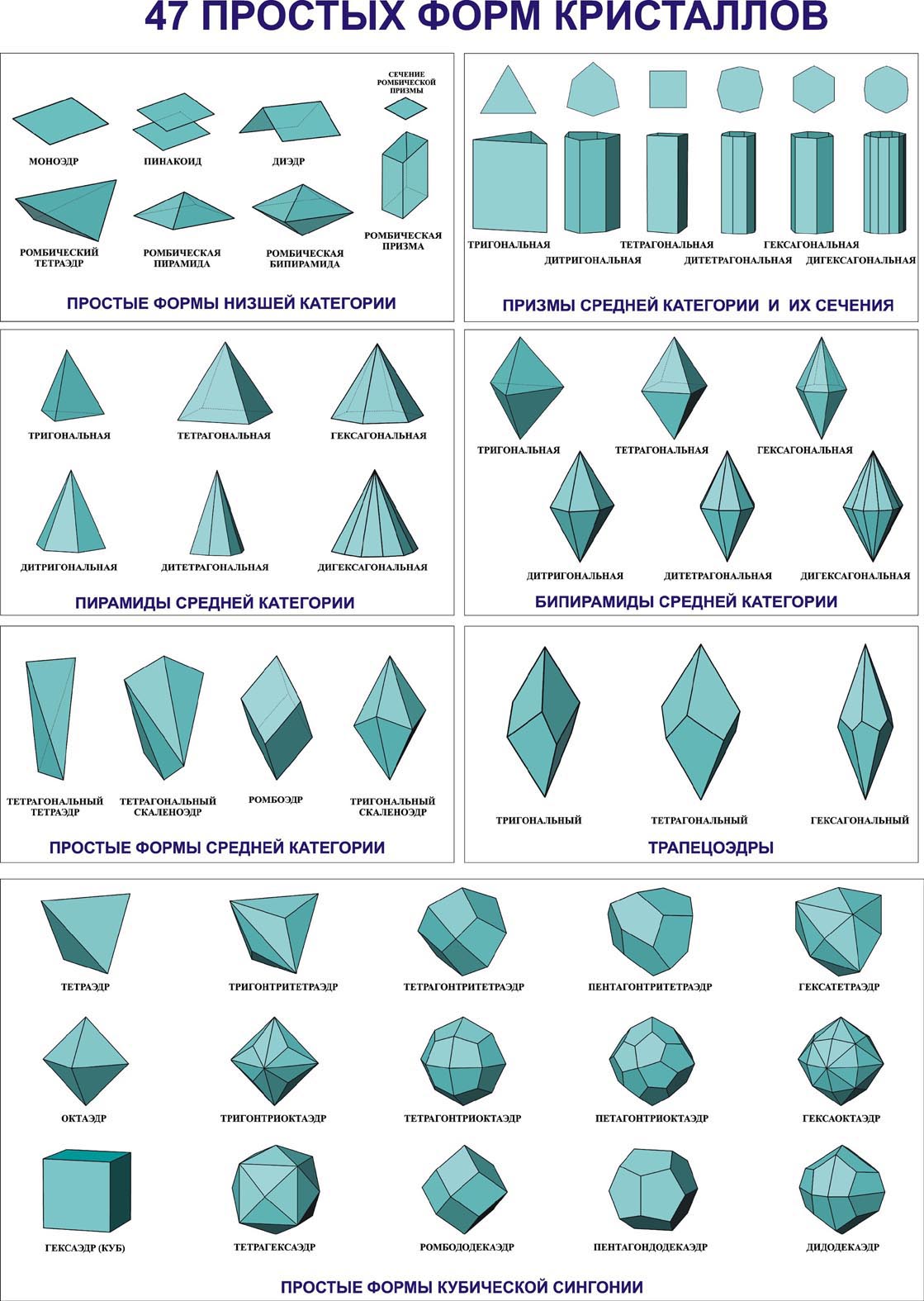
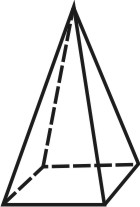
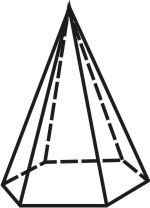
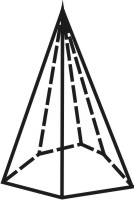
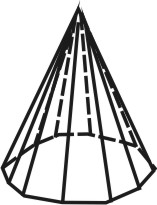
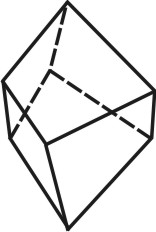
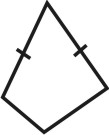
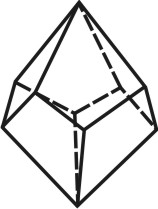
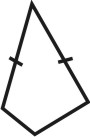
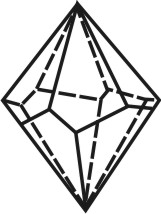
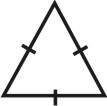
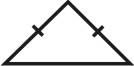
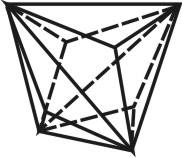
Формой многогранника называется совокупность всех его граней. Она определяется количеством всех сортов граней, взаимным расположением и соотношением размеров граней разного сорта. По внешнему виду кристаллы разделяются на две группы. К первой относятся такие кристаллы, которые состоят из одинаковых и симметрично расположенных граней (т.е. граней одного сорта). Они представляют собой простые формы. В простой форме все грани связаны между собой элементами симметрии и выводятся из одной заданной грани посредством этих элементов. Ко второй группе относятся кристаллы, обладающие различными по очертаниям и величине гранями (т.е. гранями разного сорта). Эти многогранники являются комбинациями, представляющими собой совокупность двух или нескольких простых форм. Количество простых форм, участвующих в сложении комбинационного многогранника, определяется количеством сортов граней. Всего известно 47 типов простых форм: 7 – для низшей категории, 25 – для средней и 15 – для высшей категории (таблица). Комбинаций возможно бесконечное количество.

Таблица

Характеристика простых форм

Название простой формы	Число и расположение граней	Форма граней	Изображение простой формы
Низшая категория
Моноэдр	Одна грань
Пинакоид	Две параллельные грани
Диэдр	Две пересекающиеся грани
Ромбическая призма	Четыре попарно (через одну) параллельные грани
Ромбический тетраэдр	Четыре непараллельные грани, по три пересекающиеся в каждой вершине
Ромбическая пирамида	Четыре грани, пересекающиеся в одной вершине
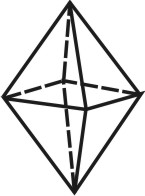
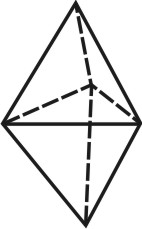
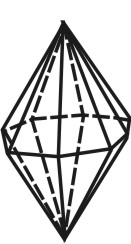
Ромбическая дипирамида	Восемь граней, располагающихся одна под другой, пересекающиеся в двух вершинах
Средняя категория
Призмы
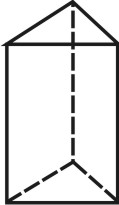
Тригональная	Три параллельные грани, в сечении треугольник
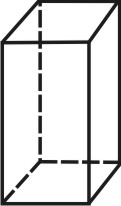
Тетрагональная	Четыре параллельные (здесь и далее относительно главной оси) грани, в сечении квадрат
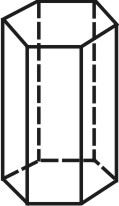
Гексагональная	Шесть параллельных граней, в сечении шестиугольник
Дитригональная	Шесть параллельных граней, в сечении дитригон (равносторонний шестиугольник, с углами, повторяющимися через один).
Дитетрагональная	Восемь параллельных граней, в сечении дитетрагон (равносторонний восьмиугольник с углами, повторяющимися через один).
Дигексагональная	Двенадцать параллельных граней, в сечении дигексагон (равносторонний двенадцатиугольник с углами, повторяющимися через один.
Пирамиды
Тригональная	Три равнонаклонные грани, пересекающиеся в одной точке на главной оси L₃.
Тетрагональная	Четыре равнонаклонные грани, пересекающиеся в одной точке на главной оси L₄.
Гексагональная	Шесть равнонаклоненных граней, пересекающиеся в одной точке на главной оси L₆.
Дитригональная	Шесть равнонаклоненных граней, пересекающихся в одной точке на главной оси L₃; в сечении дитригон.
Дитетрагональная	Восемь равнонаклоненных граней, пересекающихся в одной точке на главной оси L₄, в сечении дитетрагон.
Дигексагональная	Двенадцать равнонаклоненных граней, пересекающихся в одной точке на главной оси L₆; в сечении дигексагон.
Дипирамиды
Тригональная	Шесть равнонаклоненных граней одна под другой, пересекающихся по три в точках на главной оси L₃ (две тригональные пирамиды, сложенные основаниями).
Тетрагональная	Восемь равнонаклоненных граней, одна под другой, пересекающиеся по четыре в двух точках на главной оси L₄ (две тетрагональные пирамиды, сложенные основаниями).
Гексагональная	Двенадцать равнонаклоненных граней, одна под другой, пересекающихся по шесть в двух точках на главной оси L₆ (две гексагональные пирамиды, сложенные основаниями).
Дитригональная	Двенадцать равнонаклоненных граней, располагающихся одна под другой, пересекающиеся в двух точках на главной оси L₃ (две дитригональные пирамиды, сложенные основаниями).
Дитетрагональная	Шестнадцать равнонаклоненных граней, одна под другой пересекающихся по восемь в двух точках на главной оси L₄ (две тетрагональные пирамиды, сложенные основаниями).
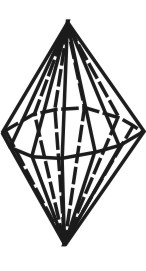
Дигексагональная	Двадцать четыре равнонаклоненных грани, одна под другой, пересекающиеся по 12 в двух точках на главной оси L₆ (две дигексагональные пирамиды, сложенные основаниями).
Тетраэдр
Тетрагональный	Четыре непараллельных грани по три пересекающиеся в каждой вершине. Нижняя грань располагается симметрично между двумя верхними (и наоборот).
Ромбоэдр
Тригональный	Шесть граней в виде ромба по три пересекающиеся в каждой вершине, нижняя грань расположена симметрично между двумя верхними (и наоборот).
Скаленоэдры
Тригональный	Двенадцать наклонных граней, пересекающих по шесть в двух точках на главной оси L₃, нижняя пара граней расположенных симметрично между двумя парами верхних.
Тетрагональный	Восемь наклонных граней, пересекающихся по четыре в двух точках на главной оси L_i₄; нижняя пара граней располагается симметрично между двумя парами верхних.
Трапецоэдры
Тригональный	Шесть наклонных граней, пересекающихся по три в двух точках на главной оси L₃; нижние грани располагаются несимметрично относительно двух верхних.
Тетрагональный	Восемь наклонных граней, пересекающихся по четыре в двух точках на главной оси L₄; нижние грани располагаются несимметрично относительно двух верхних.
Гексагональный	Двенадцать наклонных граней, пересекающихся по шесть в двух точках на главной оси L₆; нижние грани расположены несимметрично относительно двух верхних.
Высшая категория
Тетраэдры
Кубический тетраэдр	Четыре непараллельные грани, по три пересекающихся в каждой вершине.
Тригон-тритетраэдр	Двенадцать наклонных граней по три усложняющих каждую грань тетраэдра.
Тетрагон-тритетраэдр	Двенадцать наклонных граней по три усложняющих каждую грань тетраэдра.
Пентагон-тритетраэдр	Двенадцать наклонных граней по три усложняющих каждую грань тетраэдра.
Гекстетраэдр	Двадцать четыре грани, по шесть усложняющих каждую грань тетраэдра.
Октаэдры
Октаэдр	Восемь наклонных граней по четыре пересекающихся в каждой вершине.
Тригон-триоктаэдр	Двадцать четыре наклонных грани по три усложняющие каждую грань октаэдра.
Тетрагон-триоктаэдр	Двадцать четыре наклонных грани по три усложняющих каждую грань октаэдра.
Пентагон-триоктаэдр	Двадцать четыре наклонных грани по три усложняющих каждую грань октаэдра.
Гексоктаэдр	Сорок восемь граней по шесть усложняющих каждую грань октаэдра.
Гексаэдры
Гексаэдр	Шесть вертикальных и горизонтальных граней.
Тетрагексаэдр	Двадцать четыре грани по четыре усложняющих каждую грань гексаэдра.
Додекаэдры
Ромбододекаэдр	Двенадцатигранник из восьми наклонных, пересекающихся по четыре в двух точках, и четырех вертикальных граней.
Пентагондодекаэдр	Двенадцать наклонных граней, пересекающихся по три в каждой вершине.
Дидодекаэдр	Двадцать четыре грани по две усложняющие каждую грань пентагон-додекаэдра.

Простые формы бывают открытыми и закрытыми. Закрытая форма может одна образовывать кристаллический многогранник, так как грани закрытой формы полностью замыкают заключенное между ними пространство. К ним относятся дипирамиды, тетраэдры, трапецоэдры и др. Одна открытая простая форма, которыми являются, например, диэдры, пинакоиды, пирамиды и призмы, замкнутого многогранника образовать не может. Кристалл в этих случаях сформирован гранями нескольких простых форм, дающих комбинацию (не исключено, что в комбинации могут входить и закрытые формы).

Некоторые простые формы имеют две разновидности: правую и левую. Например, ромбические тетраэдры, все трапецоэдры, пентагон-тритетраэдры и др. Комбинационные многогранники также бывают правые и левые. Такие формы называют энантиоморфными (противоположно равными), это две зеркально равные фигуры, не совместимые друг с другом путем переносов и поворотов. Энантиоморфные формы возможны только в тех видах симметрии, в которых отсутствуют инверсионные оси, плоскости симметрии и центр инверсии.

آخر تعديل: الثلاثاء، 28 أبريل 2020، 12:53 PM