Стереографические проекции
Стереографические проекции
С целью наглядного пространственного положения морфологических элементов ограничения кристаллов и элементов их симметрии применяются стереографические ("стереос" – пространственный) проекции, преимущество которых заключается в том, что они дают достаточно точное представление об угловых величинах на кристаллах. Кроме того, с помощью проекций многие кристаллографические задачи решаются графическим способом.
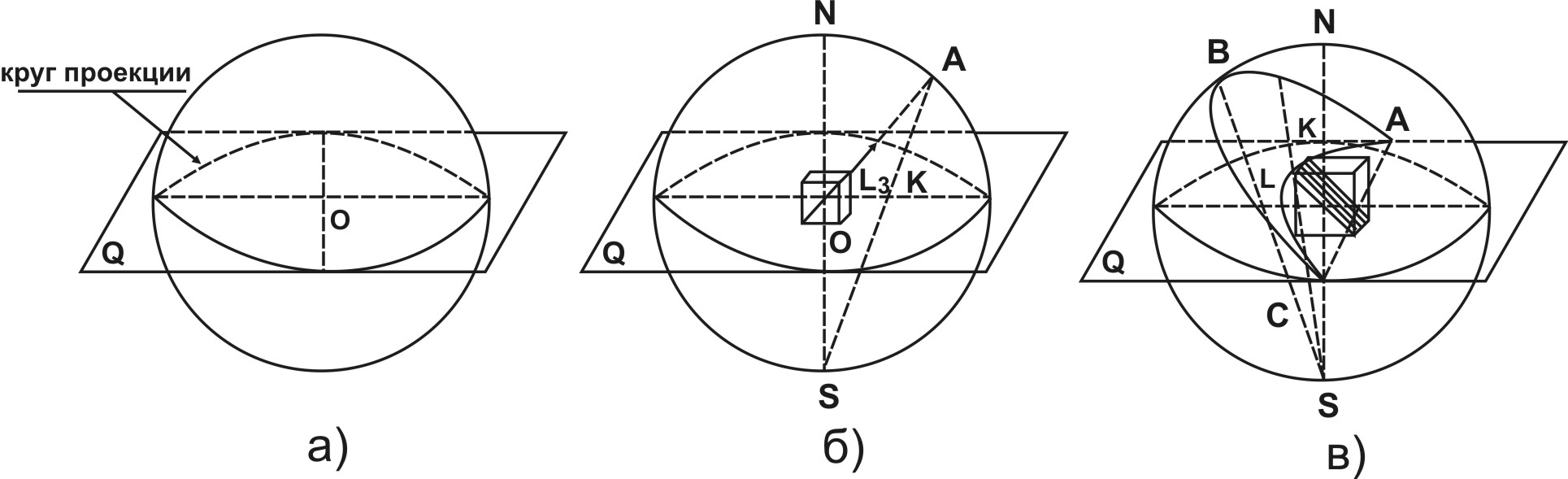
Построение проекций многогранников осуществляется на круговом сечении (называемом кругом проекции или основным кругом), которое получается в сечении сферы (или шара) проекций произвольного радиуса горизонтальной плоскостью Q. Это круговое сечение отвечает экватору сферы проекций (рис. а).
Проектирование осуществляется следующим образом. Предположим, что нам необходимо получить на круговом сечении проекцию какой-либо прямой, различным способом ориентированной в кристалле, например поворотной оси. С этой целью мысленно совмещаем центр тяжести кристалла с центром сферы проекций – точкой О. При этом кристалл должен быть определенным образом ориентирован относительно наблюдателя (см. правила установки кристаллов). Затем верхний конец этой прямой продолжаем до пересечения с поверхностью сферы. Пусть он пересекается в точке А (рис. б). Далее соединяем точку А лучом зрения АS с точкой S, за которую принимаем южный полюс сферы проекций. Луч зрения пересекается с кругом проекции в точке К, которая и является проекцией искомой прямой. Можно получить проекцию нижнего конца этой же прямой, для этого продолжают прямую вниз до пересечения со сферой и соединяют ее лучом зрения, принимая за точку зрения северный полюс сферы – N. Но, как правило, проектируют только верхний конец прямой, т.е. тот, который расположен выше плоскости проекции. Очевидно, что проекция прямой нормальной (вертикальной) к кругу проекций находиться в его центре, горизонтальной – в двух точках на круге проекции, а наклонной внутри круга. При этом, чем круче прямая (т.е. чем меньше угол между прямой и осью проекции NS), тем ближе находится точка ее проекции к центру круга и, наоборот, чем положе прямая, тем ближе располагается точка ее проекции к контуру круга.
|
|
Сфера проекций (а) и построение стереографических проекций направления (б) и плоскости (в).
Аналогичным образом получаем проекции плоскостей (в том числе плоскостей симметрии). Продолжают плоскость до пересечения ее с поверхностью сферы проекций, в результате чего получают на сфере дугу. Соединив каждую точку этой дуги лучом зрения с точкой S, имеем так называемый проектирующий конус с вершиной S. Проектирующий конус пересечет круг проекций по дуге AKLC, которая и будет стереографической проекцией плоскости ABC. Таким образом, стереографической проекцией плоскости в общем случае является дуга на круговом сечении. При этом концы дуги опираются на концы одного из диаметров основного круга проекций. Точно так же, как и в случае с прямой, проектируется только верхняя часть плоскости, лежащая над плоскостью проекций. Если проектируемая плоскость перпендикулярна к основному кругу, то ее проекция будет диаметр, по которому она пересекает круг проекций (прямая линия частный случай дуги). Если же интересующая нас плоскость горизонтальна, т.е. совпадает с плоскостью проекций, то ее проекцией будет окружность, ограничивающая круг проекций. Наклонные плоскости изображаются, как отмечалось, в виде круговых дуг внутри основного круга (в).
В стереографических проекциях изображаются элементы симметрии кристаллических многогранников, соответствующими им условными знаками (таблица).
Таблица
|
Элемент симметрии |
Расположение относительно плоскости проекции |
|
|
|
Перпендикулярно и наклонно |
Параллельно |
|
L2 |
|
|
|
L4 |
|
|
|
L3 |
|
|
|
L6 |
|
|
|
Li4 |
|
|
|
Li6 |
|
|
|
P |
|
|
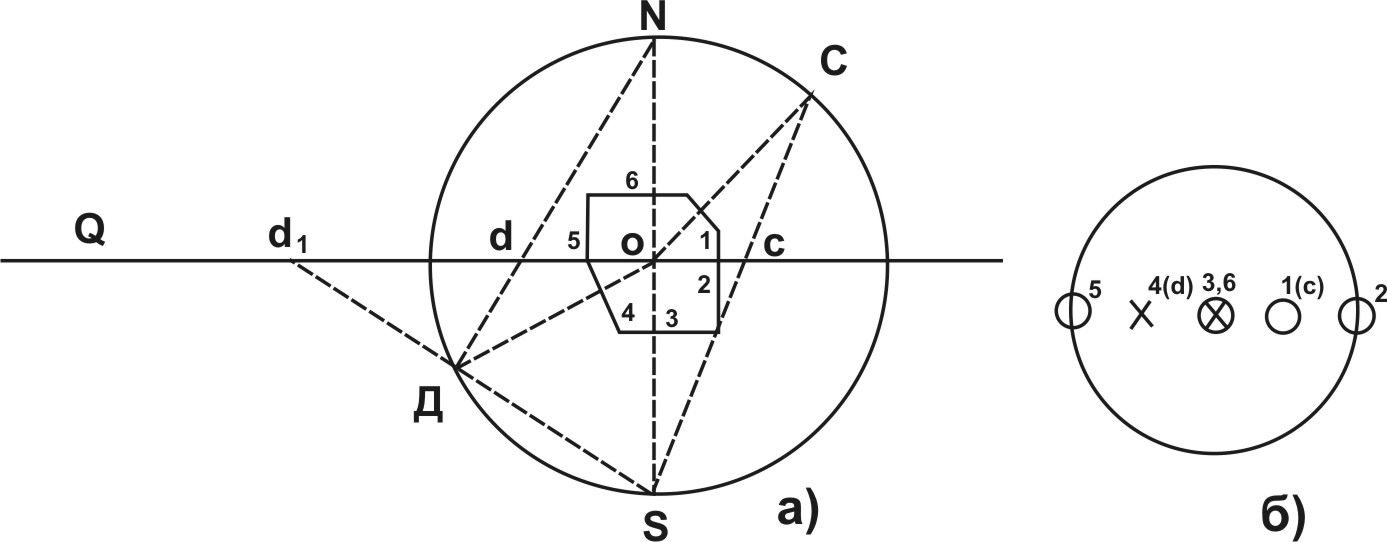
При наличии в многограннике центра инверсии - в центре круга проекций ставиться буква С. Спроектировав элементы симметрии кристалла, приступают к проектированию его граней, которые изображают в гномостереографических ("гномон" с греч. – перпендикуляр) проекциях. Особенностью этих проекций является то, что вместо данного геометрического образа проектируется перпендикулярный к нему образ. Гномостереографическая проекция грани – это стереографическая проекция перпендикуляра к ней, т.е. точка, которая получается в результате ранее описанного пространственного построения. А именно, к грани кристалла 1, находящегося в центре сферы проекций, восстанавливается перпендикуляр (если он не проходит через центр сферы, то его мысленно переносят параллельно самому себе), который продолжается до пересечения с поверхностью сферы в точке С (рисунок).
|
|
Проектирование кристалла (а); проекции граней 1 (точка с) и 4 (точка d) на плоскости Q, круг проекций (б).
Для перенесения найденной точки С на круг проекций ее соединяют лучом зрения с южным полюсом S. Получающаяся в результате пересечения луча зрения с кругом проекции новая точка "с" и является проекцией искомой грани. Заметим, что нормали к граням, пересекающие шар проекции в верхней полусфере, проектируются внутри круга проекций (например, нормаль к грани 1 (на рис.10), тогда как нормали, пересекающие шар проекций в нижней полусфере, оказываются вне этого круга – точка d1 (нормаль к грани 4 на рисунке выше).
Для того, чтобы и проекции нижних граней оказались внутри круга проекций, необходимо за точку зрения принять северный полюс N. Чтобы отличить друг от друга проекции нормалей к верхним и нижним граням, первые обозначаются кружком, а вторые – крестиками. В том случае, когда проекции граней и элементов симметрии совпадают, кружки и крестики помещают внутри знаков соответствующих элементов симметрии, которые должны иметь достаточные для этого размеры.
Необходимо хорошо усвоить, что проекции горизонтальных граней располагаются в центре круга проекций; вертикальные грани проектируются на самом круге проекций; наклонные - внутри круга, ближе или дальше от центра в зависимости от наклона грани (чем ближе грань к вертикали, тем ближе проектирующая ее точка находится к кругу проекций и, наоборот, чем больше она приближается к горизонтали, тем ближе соответственная точка к центру круга).
Кристаллографические символы
Знание элементов симметрии кристалла еще не дает однозначного представления о нем. Во многих случаях многогранники, обладающие одинаковым набором элементов симметрии, имеют совершенно разную внешнюю форму. Для более точного представления о кристалле необходимо охарактеризовать взаимное расположение его граней в пространстве. С этой целью применяются кристаллографические символы, определяющие положение любой грани данного кристалла относительно некоторых координатных осей и некоторой грани, принятой за исходную (единичную) грань.
Понятие о символах вытекает из важнейшего закона о кристаллографии, который носит разное название: з-н Гаюи, з-н целых чисел, з-н рационального отношения параметров: двойные отношения параметров, отсекаемые двумя любыми гранями кристалла на трех пересекающихся ребрах его, равны отношению целых и сравнительно малых чисел.
Установлен закон был в 1784 г.
Возьмем в кристалле 3 не // ребра пересекающихся в одной точке.
В этом же кристалле возьмем 2 не // грани, которые пересекают эти 3 ребра.
|
|
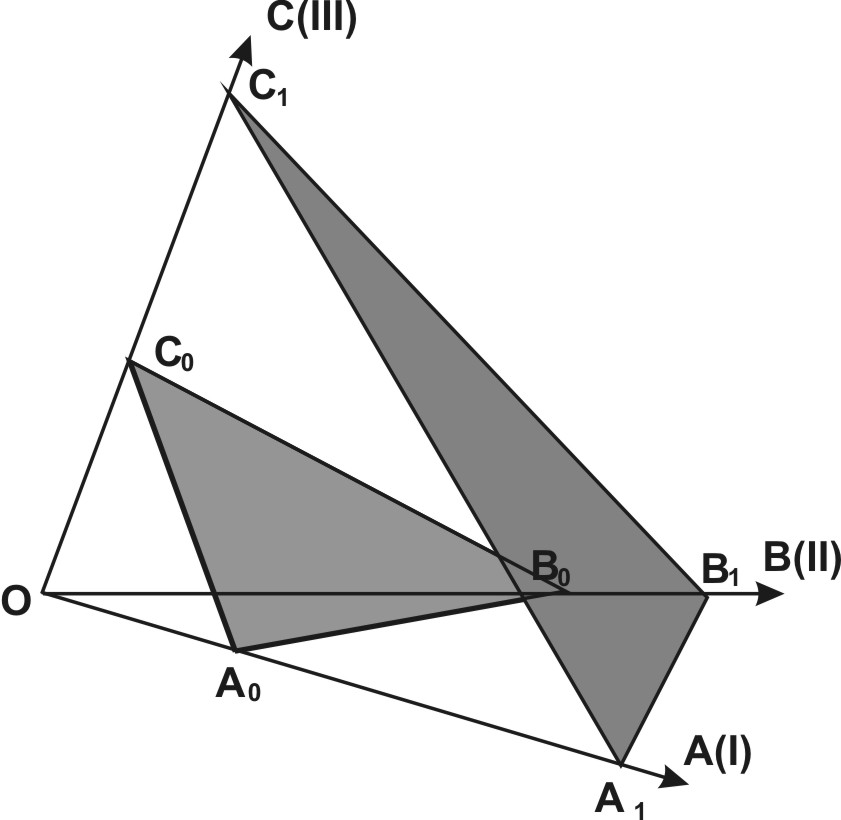
ОА (I), ОВ (II), ОС (III) – три непараллельных ребра. А0В0С0 и А1В1С1 – непараллельные грани. |
Грань А0В0С0 отсекает на ребрах отрезки ОА0; ОВ0; ОС0. Грань А1В1С1 отсекает на ребрах отрезки ОА1; ОВ1; ОС1.
Отрезки отсекаемые гранями на 3-х выбранных ребрах называются параметрами т.е. параметрами грани А1В1С1-отрезки ОС1; ОВ1; ОА1.
Оказывается, что, разделив параметры какой-либо грани на соответствующие параметры другой грани и взяв отношение между ними, получим отношения целых и сравнительно малых чисел. При этом вначале находили соотношение, предложенное Вейсом в 1818г:
ОА1 : ОВ1 : ОС1 = p:q:r
ОА0 ОВ0 ОС0
Он же вывел 2 положения:
1. Двойные отношения параметров пропорциональны целым числам
2. Получающиеся числа не велики
Закон целых чисел дает возможность охарактеризовать положение любой грани данного кристалла в пространстве при помощи чисел
Однако для числовой характеристики любой грани Ах; Вх; Сх удобнее брать обратные отношения, т.е. исходить из формулы:
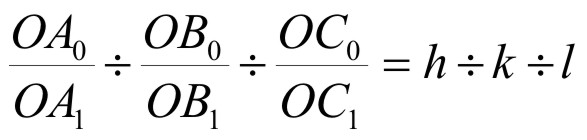
Это было принято по предложению английского ученого Миллера и эти цифры (h;k;l) отвечают положению граней в кристалле Þ символ грани АхВхСх выражаются 3-мя целыми и взаимно простыми числами, представляющими собой отношения 3-х дробей, числителями которых являются параметры единичных граней (ОА0; ОВ0; ОС0), а знаменатель соответствует параметрам заданной грани (ОАх; ОВх; ОСх).
3 числа входящие в символ называются его индексами. Первый индекс пропорционален отрезку, отсекаемым заданной гранью по первой кристаллографической оси, второй индекс пропорционально отсекается заданной гранью по 2-ой кристаллографической оси, а третий по 3-ей оси. Обозначаются без знаков препинания (hkl)
Для нахождения символов той или иной грани кристалла надо:
1. Выбрать координатные оси и единичную грань;
2. Определить величины отрезков, отсекаемых искомой гранью на осях;
3. Измерить эти отрезки соответствующими отрезками единичной грани;
4. Взять отношения, обратные найденным и привести их к целым числам.
Индексы в символе граней являются величинами обратными значениям параметров.
Выбор кристаллографических осей и единичной грани называется установкой кристалла
Полезно при этом учитывать следующие зависимости, которые существуют между параметрами грани и ее индексами:
1. Если грань отсекает по какой-либо оси отрезок больший, чем по другой оси, то индекс грани, соответствующий этой оси, меньше, чем индекс, соответствующий другой оси, и наоборот.
2. В символе грани, параллельной какой-либо кристаллографической оси, индекс, соответствующий этой оси, равен О. Если грань А1В1С1 параллельна первой кристаллографической оси Х, то отрезок, отсекаемый этой гранью, на оси равен ¥, т.е. ОА1 = ¥. Подставляя значение ОА1 в общее выражение для символов, находим:
![]()
3. Если грань пересекает отрицательный конец оси, то индекс ее по этой оси также отрицателен и над ним ставится знак минус. Например, (h-kl).
4. Символ грани отражает ее наклон к кристаллографическим осям относительно единичной грани, но не отражает расстояние грани от начала координат (параллельный перенос грани не меняет ее символа).
Например:
Первый пинакоид: (100) (-100)
Второй пинакоид (010) (0-10)
Третий пинакоид (001) (00-1)
В зависимости от положения граней относительно кристаллографических осей их символы делятся на следующие шесть типов.
1. Символ (111) всегда отвечает единичной грани, аналогичны символы (1-11), (11-1) и т.д. Заметим, что в общем случае отрезки, отсекаемые единичной гранью с символом (111) на кристаллографических осях (за исключением кубической сингонии) не равны друг другу.
2. Грань пересекает одну ось, а двум другим осям она параллельна. Символы: (100), (010), (001), (-100), (0-10) и (00-1).
3. Грань параллельна одной оси, а по двум другим – отсекает равные отрезки. По абсолютной величине эти отрезки могут быть не равными, если масштабные отрезки по осям не эквивалентны. Символы: (110), (101), (011), (-110) и т.д.
4. Грань параллельна одной оси, а по двум другим отсекает неравные отрезки. Символы: (hko), (hol), (okl), (h-ko) и т.д.
5. Грань пересекает три оси и по двум из них отсекает равные отрезки. Символы: (hhl), (hkh), (hkk), (h-kh) и т.д. Необходимо различать символы (hhl), где h>l и h<l.
6. Грань отсекает на всех осях разные отрезки. Символы: (hkl), (h-kl) и т.д.
Для гексагональной и тригональной сингоний четыре оси и записываются (hkil)
В качестве практического приложения указанных положений, вызывающих нередко затруднения, разберем несколько примеров по определению символов граней.
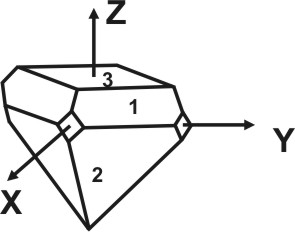
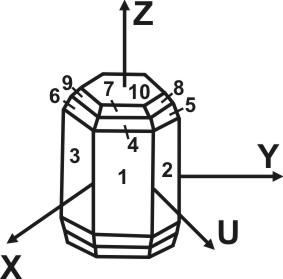
Многогранник, изображенный на рисунке, принадлежит к моноклинной сингонии и характеризуется наличием единственной оси 2-го порядка. Эту ось совмещаем со второй кристаллографической осью Y и располагаем горизонтально и параллельно наблюдателю. Ребра кристалла наиболее развитой зоны ориентируем параллельно третьей вертикальной оси Z. Первую ось – X проводим параллельно имеющемуся ребру АВ, учитывая то, что положительный конец этой оси должен быть направлен на наблюдателя и наклонен вниз, а угол a по возможности близок к 90о.
|
|
Многогранник моноклинной сингонии (L2). |
При определении символа верхней грани (1) параллельной оси Х на первое место ставим индекс – нуль; ко второй и третье оси эта грань наклонена и пересекает отрицательный конец оси Y и положительный оси Z, следовательно ее символ (o-11). Символ нижней грани (o-1-1). Все вертикальные грани параллельны третьей оси, то есть на третьем месте в записи символа надо поставить нуль. Грань, обращенная к наблюдателю (2), параллельна еще и второй оси, ее символ (100), задней оси – (-100). Грань (3), если ее мысленно продолжить, пересечет ось X и ось Y, ее символ (hko); задней (-hko). Вертикальная правая грань (4) пересекает лишь ось Y, символ ее (010), параллельной ей левой – (0-10). Символ грани (5) – (h-ko); задней (6) – (-h-ko).
На рисунке ниже изображен многогранник тетрагональной сингонии, вид симметрии L44P. Согласно правилу установки кристаллов главную ось (L4) совмещаем с осью Z, а нормали к любой паре плоскостей симметрии, находящихся относительно друг друга под прямым углом, принимаем за первую (X) и вторую (Y) кристаллографические оси. (Можно было бы выбрать не через центры маленьких граней, а через середины ребер).
|
|
Многогранник тетрагональной сингонии (L44P). |
Вертикальная маленькая грань, обращенная к наблюдателю, пересекает только первую ось, ее символ (100); аналогичная ей правая грань имеет символ (010), левая – (0-10), а задняя – (-100). Грань (1) пересекает три оси, причем на осях X и Y отсекает равные отрезки. Отрезок, отсекаемый ею по оси X, будет служить единицей измерения и по оси Y, так как у тетрагональных кристаллов a0 = b0. Следовательно, правильно будет ее символом обозначить (hhl). Таких граней четыре. Их символы различаются знаками (h-hl), (-hhl), (-h-hl). Грань (2), принадлежащая нижней пирамиде, имеет такой же наклон к осям, как и грань (1). Ее символ отличается от символа грани (1) только отрицательным знаком третьего индекса – (hh-l), точно так же как и символы других аналогичных ей граней – (h-h-l), (-hh-l) и (-h-h-l). Верхняя горизонтальная грань (3), параллельная первым двум осям и отсекающая отрезок лишь по оси Z, имеет символ (001).
И, наконец, рассмотрим кристалл гексагональной сингонии, вид симметрии L66L27PC. L6 совмещаем с осью Z. Оси X, Y и U ориентируем по трем осям 2-го порядка, располагающимся под углом 60о друг к другу. Можно выбрать либо тройку L2 нормальных к вертикальным граням, либо к ребрам. Предпочитаем последний вариант.
|
|
Многогранник гексагональной сингонии (L66L27PC). |
Ось Y ориентируем параллельно наблюдателю. Грань (1) отсекает равные отрезки на положительном конце оси X и отрицательном конце оси U, при этом оказывается параллельной оси Z и второй оси Y. Отсюда ее символ (ho-ho), или более правильно (10-10). Таких граней шесть, каждая из них пересекает два разных конца 3-х горизонтальных осей, различающихся знаками. Символ грани (2) – (01-10), грани (3) - (1-100); соответственно задних граней слева направо: (0-110), (-1010) и (-1100). Грани типа 4, располагающиеся выше и ниже относительно вертикальных граней, ориентированы аналогично им по отношению к горизонтальным осям, но еще наклонены к четвертой оси. Их символы: 4 – (ho-hl), 5 – (oh-hl), 6 – (h-hol); символы нижних граней отличаются лишь отрицательными значениями четвертого индекса – соответственно - (ho-h-l), (oh-h-l) и (h-ho-l). Грань (4) отвечает условию единичной грани. Горизонтальные верхняя (10) и нижняя грани, отсекающие отрезки на оси Z, характеризуются символами (0001) и (000-1).
Закон поясов
(Вейса)
Поясом (или зоной) называется совокупность граней кристалла, пересекающихся в параллельных ребрах. На рисунке грани (2), (3), (4), (5) принадлежат одному поясу.
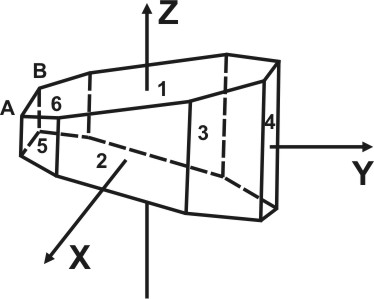
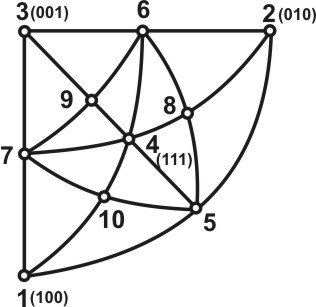
Осью зоны называется направление, параллельное всем ребрам зоны (на рисунке ось зоны совпадает с осью Z). Проекцией оси зоны является проекция плоскости, нормальной к ее оси, которая изображается в общем случае дугой большого круга. Само собой разумеется, что все проекции граней данного пояса представлены точками на проекции самой зоны. Закон поясов (закон Х.С. Вейса) формулируется следующим образом: точка пересечения проекций любых двух зон кристаллов является проекцией возможной грани. С помощью этого закона теоретически выводятся возможные грани и ребра кристаллов. Пусть на проекции (рис.) заданы четыре непараллельные грани кристалла – 1, 2, 3, 4. Через каждые две грани проводим дугу большого круга, соответствующую проекции пояса.
|
|
Вывод возможных граней методом развития зон. |
Пояса 1-2 и 3-4, 2-3 и 1-4, 1-3 и 2-4 пересекаются в точках 5, 6, 7, которые представляют собой проекции возможных граней. Через них можно провести новые зоны (5-6, 6-7 и 7-5) и получить новые точки пересечения зон (8, 9, 10). Соединяя дугами больших кругов и эти точки, получаем зоны, которые, пересекаясь с ранее выведенными поясами, дают серию новых возможных граней и т.д. Этот графический способ вывода возможных граней называется "методом развития зон".
Зная символы четырех исходных граней кристалла, легко определить и символы найденных возможных граней. Для этого применяют два метода: а) метод "перекрестного умножения" и б) метод сложения и вычитания индексов.
В первом случае для определения символа возможной грани 5 предварительно определяют символы поясов 1-2 и 3-4, на пересечении которых эта грань находится. Символ пояса отвечает символу ребра, лежащего на пересечении граней данного пояса. В поясе 1-2 лежат две грани с символами (100) и (010), отсюда определяем символ ребра (пояса)
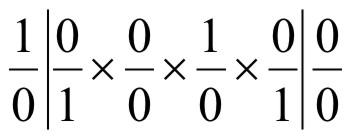
(0 × 0 – 1 × 0) : (0 × 0 – 0 × 1) : (1 × 1 – 0 × 0) = 0 : 0 : 1 [001]
Аналогичным путем, зная символы граней 3 – (001) и 4 – (111), определяем символ пояса, проходящего через эти грани. Имеем – [-110]. Далее, применяя правило перекрестного умножения, исходя из символов двух ребер (поясов), определяем символ искомой грани 5, проходящей или параллельной этим ребрам.
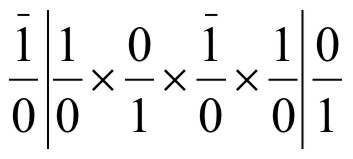 (110)
(110)
Для определения символа грани по символам двух зон в зависимости от того, какой из них ставился вверху, а какой внизу, вообще получается два результата: или искомый символ, или символ параллельной грани. Они различаются друг от друга лишь противоположными знаками всех индексов.
Второй метод основан на зависимости, найденной В. Гольдшмидтом, которая гласит, что все грани, связанные поясами, могут быть выведены из двух граней пояса сложением и вычитанием символов граней. Если определяется символ грани, находящейся между двумя другими гранями, то индексы последних складываются. Пример: грань 5 (рис.18) лежит в поясе 1-2 между гранями (100) и (010). Сумма индексов (100 + 010) = 110 дает символ грани 5. При определении символа грани, находящейся слева или справа от граней с известными символами, последние вычитаются. Пример: то же символ грани 5 – (110), лежащей в зоне 3-4, можно получить, если (111-001) = 110.